数据结构之各种树(二叉树、AVL树、红黑树、B、B+树)
二叉查找树
性质:
1、任意节点左子树不为空,则左子树的值均小于根节点的值;
2、任意节点右子树不为空,则右子树的值均大于于根节点的值;
3、任意节点的左右子树也分别是二叉查找树;
4、没有键值相等的节点;
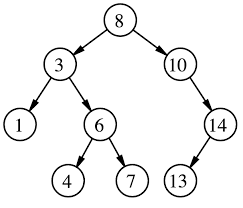
图示:
二叉查找树按照中序遍历即从小到大分布:1,3,4,6,7,8,10,13,14
 ‘
‘
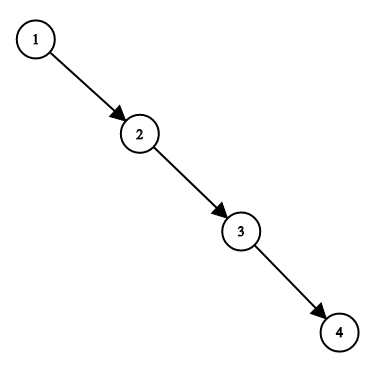
局限:
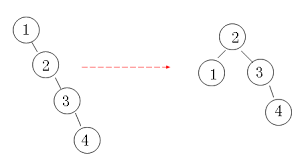
极端情况如下,会退化成为一个N个急待你的线性链表
AVL树(二叉平衡树)
性质:
1、满足二叉查找树的性质
2、平衡条件必须满足(所有节点的左右子树高度差不超过 1)。
不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是非常耗时的,由此我们可以知道 AVL 树适合用于插入删除次数比较少,但查找多的情况。
图示:
局限性:
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么 AVL 还是较优于红黑树。
红黑树
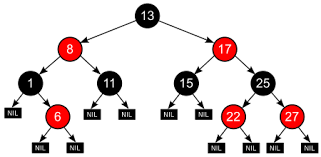
性质:
- 每个节点非红即黑;
- 根节点总是黑色的;
- 每个叶子节点都是黑色的空节点(NIL节点);
- 如果节点是红色的,则它的子节点必须是黑色的(反之不一定);
- 从根节点到叶节点或空子节点的每条路径,必须包含相同数目的黑色节点(即相同的黑色高度)。
图示:
应用:
TreeMap,TreeSet以及JDK1.8的HashMap底层
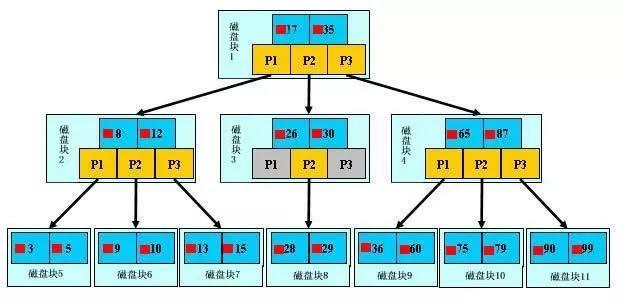
B树
性质:
1、定义任意非叶子结点最多只有 M 个儿子,且 M>2;
2、根结点的儿子数为 [2, M];
3、除根结点以外的非叶子结点的儿子数为 [M/2, M];
4、每个结点存放至少 M/2-1(取上整)和至多 M-1 个关键字;(至少 2 个关键字)
5、非叶子结点的关键字个数 = 指向儿子的指针个数 - 1;
6、非叶子结点的关键字:K [1], K [2], …, K [M-1];且 K [i] < K [i+1];
7、非叶子结点的指针:P [1], P [2], …, P [M];其中 P [1] 指向关键字小于 K [1] 的子树,P [M] 指向关键字大于 K [M-1] 的子树,其它 P [i] 指向关键字属于 (K [i-1], K [i]) 的子树;
8、所有叶子结点位于同一层;
图示:
B+树
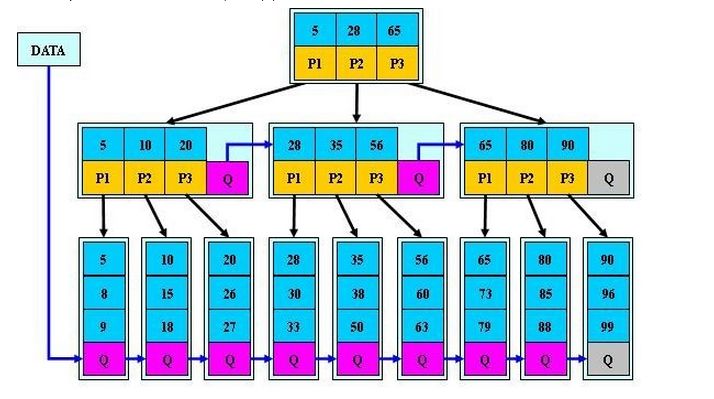
性质:
1、非叶子节点的子树指针与关键字个数相同;
2、非叶子节点的子树指针 p [i], 指向关键字值属于 [k [i],k [i+1]] 的子树.(B 树是开区间,也就是说 B 树不允许关键字重复,B + 树允许重复);
3、为所有叶子节点增加一个链指针;
4、所有关键字都在叶子节点出现 (稠密索引). (且链表中的关键字恰好是有序的);
5、非叶子节点相当于是叶子节点的索引 (稀疏索引), 叶子节点相当于是存储 (关键字) 数据的数据层;
6、更适合于文件系统;
图示:
应用:
B和B+树主要用作文件系统以及数据库做索引
B 树& B+树区别
- B 树的所有节点既存放键(key) 也存放 数据(data),而 B+树只有叶子节点存放 key 和 data,其他内节点只存放 key。
- B 树的叶子节点都是独立的;B+树的叶子节点有一条引用链指向与它相邻的叶子节点。
- B 树的检索的过程相当于对范围内的每个节点的关键字做二分查找,可能还没有到达叶子节点,检索就结束了。而 B+树的检索效率就很稳定了,任何查找都是从根节点到叶子节点的过程,叶子节点的顺序检索很明显。
参考:https://learnku.com/articles/52909

