第328场周赛
简单题,暴力即可。
num%10代表获取该数的个位数字
num/10代表该数缩小10倍,原个位数字抹掉了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public class Solution01 {
public int differenceOfSum(int[] nums) {
int sum1 = 0;
int sum2 = 0;
for(int i =0;i<nums.length;i++){
sum1+= nums[i];
while(nums[i] !=0 ){
sum2 += nums[i] % 10;
nums[i] = nums[i] / 10;
}
}
return Math.abs(sum1-sum2);
}
}
|
一维前缀和:int[] prefixSum用于用于存储前缀和数组,prefixSum[i]代表nums[0,i-1]之和;任意区间nums[l,r]之和为prefixSum[r+1]-prefixSum[l]。可用于一维数组任意区间快速求和,时间复杂度O(1)
相关题目:303. 区域和检索 - 数组不可变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public class Solution02_303 {
class NumArray {
int[] prefixSum;
public NumArray(int[] nums) {
prefixSum = new int[nums.length+1];
for(int i =1;i<prefixSum.length;i++)
prefixSum[i] = prefixSum[i-1]+nums[i-1];
}
public int sumRange(int left, int right) {
return prefixSum[right+1]-prefixSum[left];
}
}
}
|
一维差分:结合一维前缀和的公式,如果需要对任意区间nums[l,r]进行加操作,只需对prefixSum[r+1]加操作且prefixSum[l]进行减操作,反之亦然。可用于快速对一维数组的任意区间进行加/减操作,时间复杂度O(1)
二维前缀和:可用于二维数组任意区间快速求和,时间复杂度O(1)
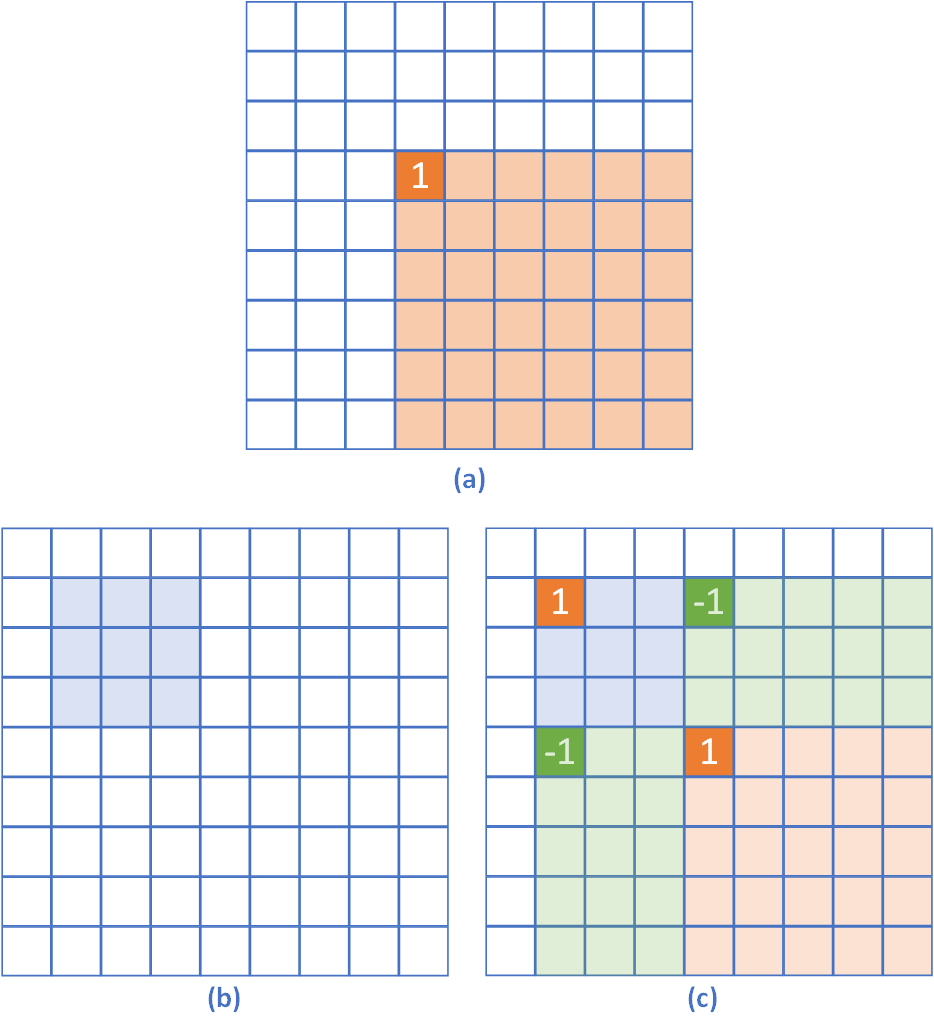
相关题目:304. 二维区域和检索 - 矩阵不可变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public class Solution02_304_2 {
static class NumMatrix {
int[][] matrixSum;
public NumMatrix(int[][] matrix) {
matrixSum = new int[matrix.length+1][matrix[0].length+1];
for(int i = matrix.length-1;i>=0;i--){
for(int j = matrix[0].length-1;j>=0;j--){
matrixSum[i][j] = matrix[i][j] + matrixSum[i+1][j]+matrixSum[i][j+1]-matrixSum[i+1][j+1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return matrixSum[row1][col1]-matrixSum[row2+1][col1]-matrixSum[row1][col2+1]+matrixSum[row2+1][col2+1];
}
}
}
|
二维差分:可用于快速对二维数组的任意区间进行加/减操作,时间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public class Solution02 {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] diff = new int[n+1][n+1];
for(int i = 0;i<queries.length;i++){
diff[queries[i][0]][queries[i][1]]++;
diff[queries[i][0]][queries[i][3]+1]--;
diff[queries[i][2]+1][queries[i][1]]--;
diff[queries[i][2]+1][queries[i][3]+1]++;
}
for(int i=0;i<n;i++)
for(int j=1;j<n;j++) diff[i][j]+=diff[i][j-1];
for(int i=1;i<n;i++)
for(int j=0;j<n;j++) diff[i][j]+=diff[i-1][j];
int[][] ans = new int[n][n];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) ans[i][j] = diff[i][j];
return ans;
}
}
|
同向双指针,由Map保存窗口中的数字出现的次数,窗口中相等值的的数目为pairs。
首先枚举子数组右端点right,那么paris增加map.getOrDefault(nums[right],0);枚举至paris>=k即代表该窗口中子数组符合好子数组;然后看左端点left端点最大可以到多少,如果去掉左端点,pairs没有小于k,就可以移动左端点。
由于左端点及其左边的都可以是好子数组的左端点,所以每个右端点对应的答案个数为left+1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public class Solution03 {
public long countGood(int[] nums, int k) {
Map<Integer,Integer> map = new HashMap<>();
long ans = 0;
int pairs =0,left = 0;
for(int num : nums){
pairs += map.getOrDefault(num,0);
map.merge(num,1,Integer::sum);
while(pairs-map.get(nums[left])+1>=k){
pairs -= map.merge(nums[left++],-1,Integer::sum);
}
if(pairs>=k) ans+=left+1;
}
return ans;
}
}
|
待做~


